pomocy ziri: W kwadracie ABCD wierzchołek A ma współrzędne (2,0), a jedna z przekątnych zawiera się w prostej o równaniu y=2x+1 Oblicz a)długosc d przekątnej kwadratu b)pole kwadratu prosze o szybka pomoc!

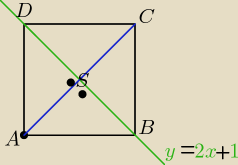
Eta: 1 sposób: sprawdzamy czy punkt A(2,0) należy do tej przekątnej 0≠ 2*2+1 zatem punkt A nie należy do tej prostej y= 2x+1 odległość IASI punktu A od tej prostej jest równa połowie długości przekątnej tego kwadratu bo przekątne w kwadracie są równe i prostopadłe prosta: y=2x+1 w postaci ogólnej: 2x−y+1=0 i A(2,0)

	I2*2−0*1+1I		5		5√5
to: IASI =		=		=		= √5
	√22+(−1)2		√5		5

to długość przekątnej IACI= 2*IASI= 2√5 IACI= a√2 −−− dł. przekątnej kwadratu o boku "a" zatem: a√2= 2√5

	2√5		2√10
a=		=		= √10
	√2		2

to: P=a²= 10 [j²]